三角比の覚え方から近似値を導出してみる
三角比の覚え方から近似値を導出してみる
Twitterをみていると、三角比の覚え方についてのPostが流れてきました。

三角比でよく出てくる角度0°,30°,45°,60°,90°に0,1,2,3,4と割り振ると、ルートをつけて2で割るだけでsinの値が求まる!簡単!
画期的だと言う声もある一方
三角定規の比率1:1:√21:2:√3を覚えた方が本質的では?
や
角度を恣意的に決めており、三角関数と何の関係もないから数学でやる意味がない
との批判の声もあります。この覚え方を教えることの是非はここでは論じませんが、
等間隔でない数列に意味がないわけではないし、もしかしたらここから良い三角関数の近似式が求められ、そこからさらに三角関数への理解が深まる可能性があります。
テイラー展開とは
三角関数を多項式近似するというと、テイラー展開が浮かびます。
sin(x) をテイラー展開してみると、
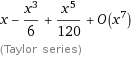
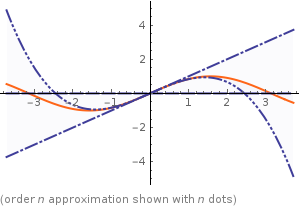
例えば45° (=π/4)の時、3次、5次のテイラー展開を求めてみると
√2/2= 0.70710678118に対し、
((π/4)-(π/4)^3/6+(π/4)^5/120)= 0.7071430
と階乗のオーダーでどんどん近づいていきます。
近似式を求める
まずはパラメータzを使って、先ほどの表を媒介変数表示してみましょう。
| z | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 1/2 | √2/2 | √3/2 | 1 |
| x | 0 | π/6 | π/4 | π/3 | π/2 |
こちらを規則性がわかるように書き直すとこうなります。
| z | 0 | 1 | 2 | 3 | 4 |
| y | √0/2 | √1/2 | √2/2 | √3/2 | √4/2 |
| x | 0*π/12 | 2*π/12 | 3*π/12 | 4*π/12 | 6*π/12 |
yについては、
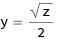
と表せるとして、0,2,3,4,6と変化するxをどのように表現するかが問題です。
0,2,3,4,6 について、
差分をとると、+2,+1,+1,+2
とz = 2を基準に増分が対称的になっています。
- 差分が線対称
- 数列が単調増加
と言うことで、ここでは、3次関数で表現してみます。
z:-2,-1,0,1,2
x:-3,-1,0,1,3
を通る三次関数の原点を(2,3)に移動させた
x = (z^3-6z^2+17z)/6
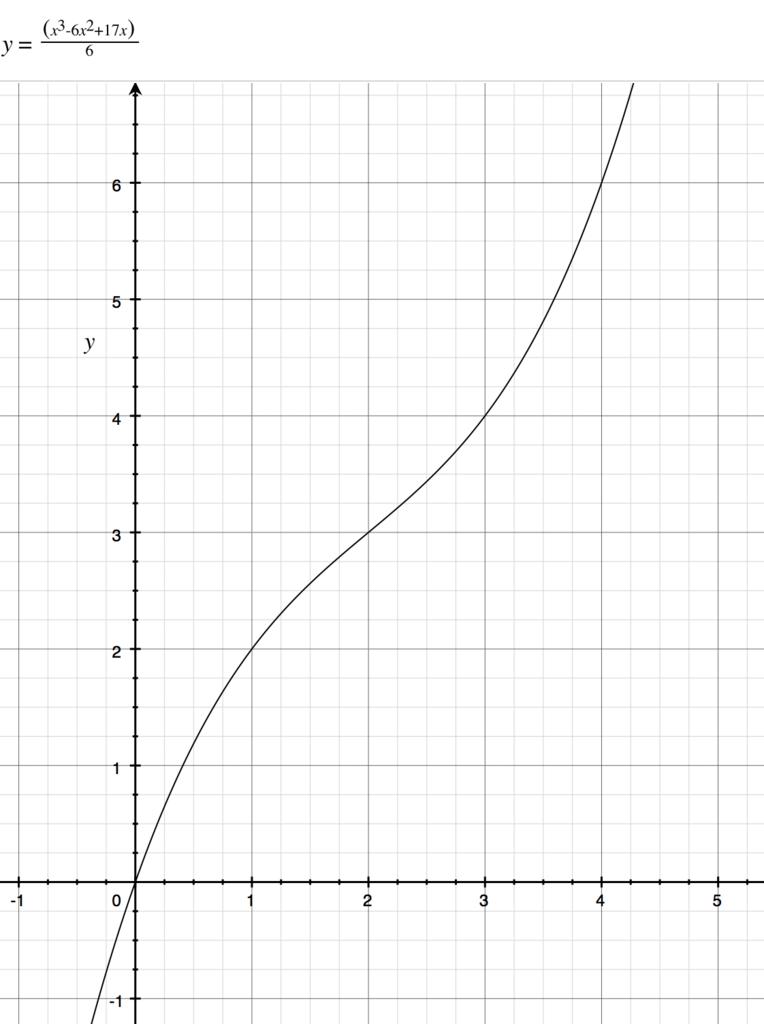
これにπ/12を掛けて
x = (z^3-6z^2+17z)*π/72
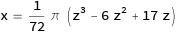
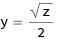
y = √z/2z = 4y^2
から、zを消去して
x = (64y^6-96y^4+68y^2)π/72= (16y^4-24y^2+17)y^2*π/18
ということで
y = sin(x) の逆関数、すなわちy = arcsin(x)の近似多項式
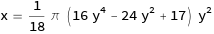
を手に入れました。
つまり、この逆関数を求めればy = sin(x) (x = 0 to π/2)の近似関数が求まるはず
...ですが、解く気がしないのでWolfram先生にお伺いを立てます。
こちらが実数係数の逆関数になります。

これで、sin30°の値を忘れても、この数式さえ覚えていれば、x = π/6を代入すれば1/2と、値を知ることができます。
さっきの三角比の表から近似式を出そうとあれこれした結果こうなりました。
— Hiroaki Hosono (@wand125) 2017年12月3日
これで、sin30°の値を忘れても、この数式さえ覚えていれば、
x = π/6を代入して、値を知ることができます。 pic.twitter.com/NicBFTguB8
もう少し簡潔にまとめることもできそうですが、これ以上のこちらの考察は置いておき、
逆関数、y = (16x^4-24x^2+17)x^2*π/18の特徴をみていきましょう。
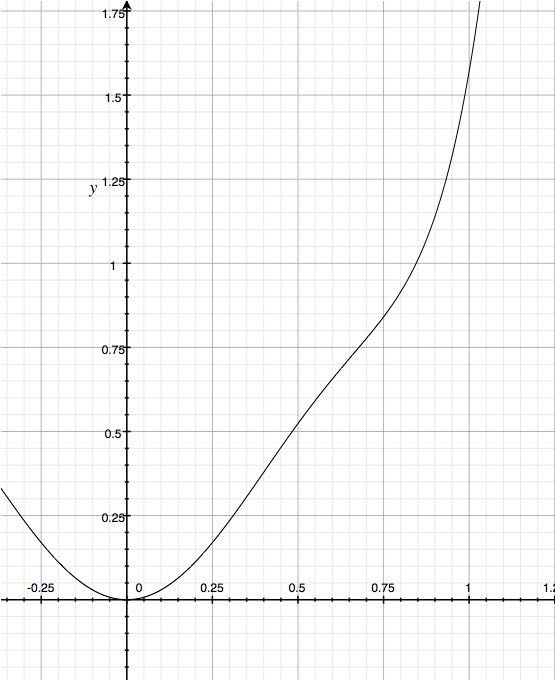
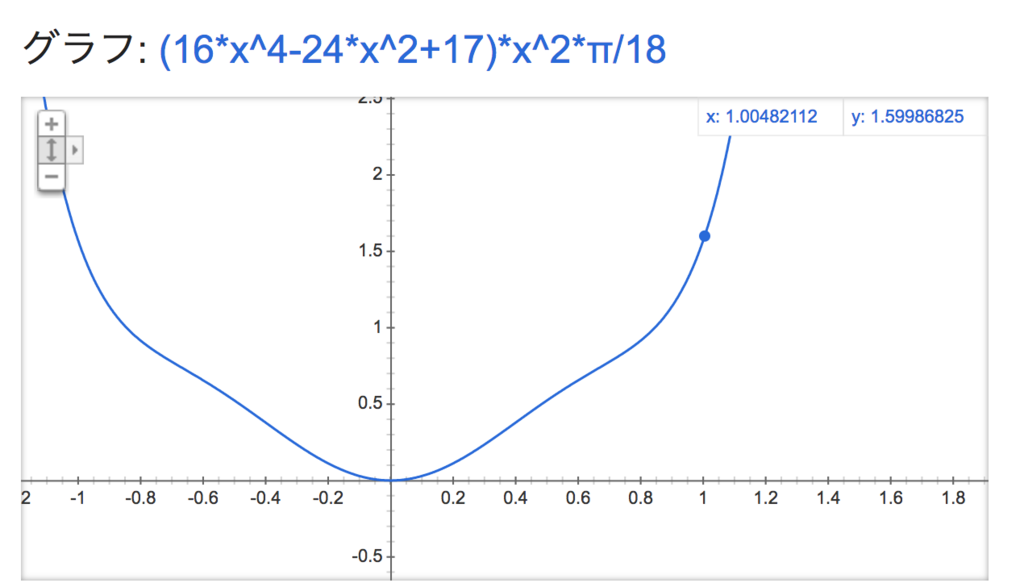
かっこ悪い形ですが、指定した点を通るように多項式を作ったら上に凸なところと下に凸なところができてしまうのは仕方ありません。重要なのはこの関数がy = arcsin(x)をどれほど近似できているかです。
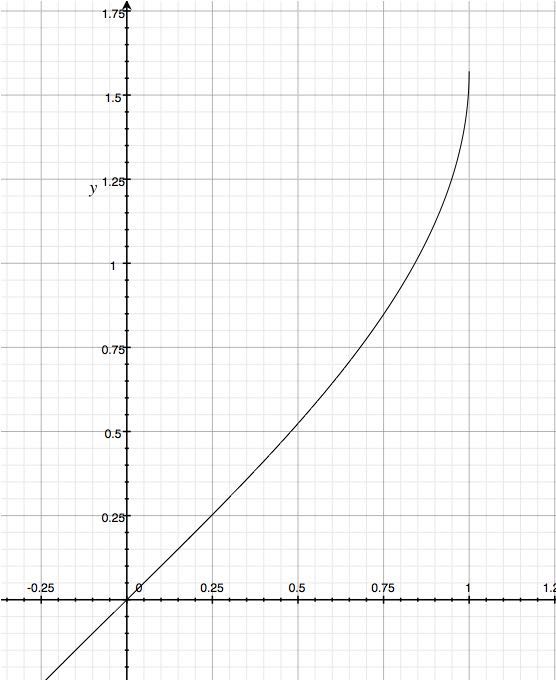
y = arcsin(x)のグラフ
重ねたグラフ
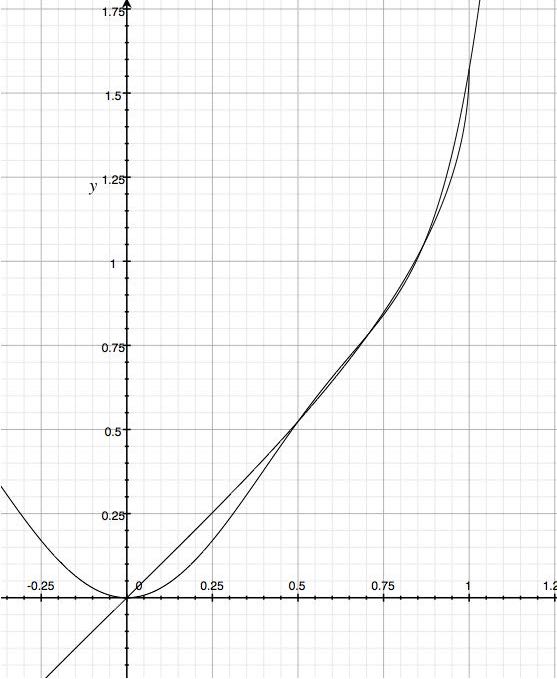
1/2〜√3/2(=0.866)の区間はほぼ一致、それ以外の場所はズレまくり、という結果に。45°周辺のsinの値を求めるには良いかもしれません。
ちなみに、arcsin(x) (|x| < 1)を5次でテイラー展開すると
となりとても綺麗な近似曲線が現れます。

どれくらいの誤差があるかの比較のため、1/2, √2/2近辺の値を比較してみます。
arcsin(1/2*101/100) = 0.529381965
近似多項式(6次) = 0.5235987
テイラー展開(5次) = 0.528927
arcsin(√2/2*101/100) = 0.79544884
近似多項式(6次) = 0.79417127751
テイラー展開(5次) = 0.78882347389
テイラー展開(7次) = 0.79305402176
arcsin(1/2 √(2 + √(2 - √(3))))
= arcsin(0.7933533402)
= 7π/24
= 0.916297857
近似多項式
0.90438123
テイラー展開(5次)
0.9001492619
テイラー展開(7次)
0.908980438389
なんと、√2/2 近辺ではこの近似多項式の方が精度が高いという結果に。
テイラー展開は途中まで精度高く近似できますが、
高次になるほどxが1に近くにつれ急激にx^nの値は大きくなるため、
1に近づく部分はテイラー展開でもなかなか近似できないようです。
テイラー展開にぼろ負けするオチかと思いきや、